大家好，今天我们来聊聊傅里叶级数。这可不是一个遥不可及的高深话题，它其实是现代数学、物理和工程学中非常基础且重要的工具。说到傅里叶级数，很多人可能会想到复杂的公式和抽象的数学空间，但其实它背后有一套非常简单、直观的数学思想。接下来，我们就从简单的三维向量讲起，一步步扩展到希尔伯特空间，最后再揭示傅里叶级数和傅里叶变换的本质。
本文由中科声玄（苏州）科技有限公司技术团队撰写，致力于用通俗易懂的方式，帮助大家理解信号处理背后的数学原理。
一、三维向量与几何直观
在高中学习的三维立体空间中：向量内积
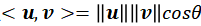
它定义了向量的夹角，投影，长度和正交性。向量分解：任意向量都能分解到一组正交基上。例如
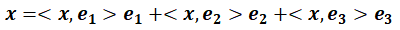
这奠定了一个基本观念：基 + 内积 → 向量的几何分解。
二、向量空间的推广：从三维到无限维
“向量”让人联想到三维空间中有方向、有长度的箭头，但在抽象数学中，“向量”的含义推广了，“向量”可以是函数、多项式、矩阵等任何满足运算规则的对象。
1. 向量空间的定义
一个向量空间是一个集合，它包含向量元素并且定义了向量加法和标量乘法操作。如果这些操作满足一定的公理（比如交换律、结合律、单位元等），那么这个集合就是一个向量空间。
2. 抽象“向量”的例子
统一逻辑：“向量”不是几何上的箭头，而是抽象的对象，只要它们满足加法与数乘的线性运算规则，就构成一个向量空间。维数可以是有限的（矩阵、多项式截断）或无限的（全体多项式、函数空间）。
三、为无限维向量空间配备工具：希尔伯特空间的诞生
希尔伯特空间是一个非常重要的概念，它是无限维向量空间的一种扩展。通过引入范数、内积和完备性，希尔伯特空间为我们提供了更加丰富的空间结构，为无限维向量空间配备工具。
核心思想：从“由元素构成空间”到“赋予空间结构”。
1. 无限维向量空间：只有线性结构，无长度、角度与收敛概念。
2. 赋范空间：引入范数
，可以测量长度与距离，从而谈收敛。
3. 内积空间：引入内积< x,y>，可以定义角度、正交与投影，内积诱导范数。
4. 希尔伯特空间：完备的内积空间，保证柯西序列的极限仍在空间内。
直观比喻——
(1)向量空间：一片空旷的土地。
(2)赋范空间：我们在土地上放置了尺子，能测量长度。
(3)内积空间：有了尺子和量角器。
希尔伯特空间：土地平整无坑，任何极限都“落得下来”。
希尔伯特空间的一个经典例子就是平方可和的数列空间（ 
空间）和平方可积函数空间（ 
([a,b])空间）。这些空间不仅有向量加法和标量乘法操作，还能定义距离、角度等结构。
现在，你通过我的讲解了解了希尔伯特空间这一重要概念。希尔伯特空间是一个非常深刻且重要的数学物理主题。从无限维向量空间到希尔伯特空间的演变，是现代分析学、量子力学和许多工程领域的基石。
四、终极分解：希尔伯特空间中的函数分解与傅里叶级数
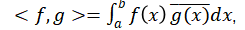
这正是傅里叶级数。换句话说：
傅里叶级数 = 希尔伯特空间里的一次基展开。
（路径二：更优美的复指数形式）
进一步，将以上改写为复指数形式：
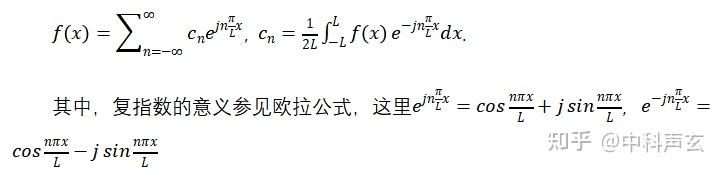
五、傅里叶级数到傅里叶变换
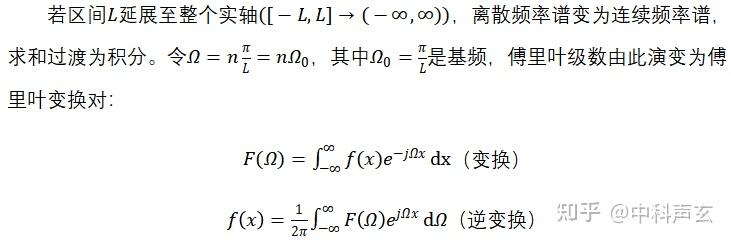
六、路线回顾
1. 三维空间中的向量分解提供了直观起点。
2. 向量空间推广统一了多项式、矩阵、函数等对象。
3. 无限维空间逐步引入范数、内积与完备性，得到希尔伯特空间。
4. 希尔伯特空间中的基展开对应傅里叶级数。
5. 区间推广与频率连续化带来了傅里叶变换。
七、总结与启示
向量并不仅仅是几何上的箭头，它还可以是多项式、矩阵、函数等。
无限维空间的构建需要逐步加上范数、内积和完备性，最终形成希尔伯特空间。
傅里叶级数其实是希尔伯特空间中的基展开，而傅里叶变换则是它的自然推广
最后一条总结：
傅里叶级数和傅里叶变换，实际上是希尔伯特空间中“向量=基展开”思想的直接产物
八、应用举例
1. 信号处理：在数字通信中，信号常通过傅里叶变换转换到频域，以滤波、调制、压缩。快速傅里叶变换（FFT）正是这种理论的工程化成果。
图像处理：图像压缩（如 JPEG）利用离散余弦变换（DCT），其本质就是傅里叶展开的变形。
1. 量子力学：波函数属于希尔伯特空间，傅里叶变换连接了位置表象和动量表象，揭示了不确定性原理的数学根基。
2. 振动与声学：乐器发出的复杂声音可分解为不同频率的谐波，这就是傅里叶级数的物理直观解释。
本文由中科声玄（苏州）科技有限公司技术团队撰写，致力于用通俗易懂的方式，帮助大家理解信号处理背后的数学原理。我们下期再见。
